Hier erkläre ich den Zusammenhang zwischen der Brennweite und der Vergrößerung einer konvexen Sammellinse. Es erfolgt immer sowohl eine grafische Darstellung, als auch eine rechnerische Beweisführung.
Wie wirkt sich die Brennweite einer Linse auf deren Vergrößerungsfaktor aus?
Bei der optischen Abbildung von Objekten bedeutet eine große Brennweite eine höhere Vergrößerung.
Vergrößert man jedoch als virtuelles Bild, dann ist eine kurze Brennweite besser. Es kommt darauf an, ob das Objekt innerhalb oder außerhalb der Brennweite platziert wird:
Objekt außerhalb der Brennweite – relles Bild
Den Zusammenhang zwischen der Brennweite und der Vergrößerung einer Linse bei der optischen Abbildung kann man sich recht schnell anhand der Linsengleichung erschließen. Allerdings ist das sehr abstrakt und ich möchte abseits vom Zahlenwerk eine grafische Veranschaulichung zu diesem Thema bieten. So lässt sich die Systematik viel leichter einprägen als lange über eine komplizierte Formel zu grübeln und jedesmal neu rechnen zu müssen, sobald sich eine Variable ändert. Bei der Abbildung eines Objektes als reelles Bild gelten folgende Regeln:
Regel 1: Je größer die Brennweite der Linse, desto höher die Vergrößerung
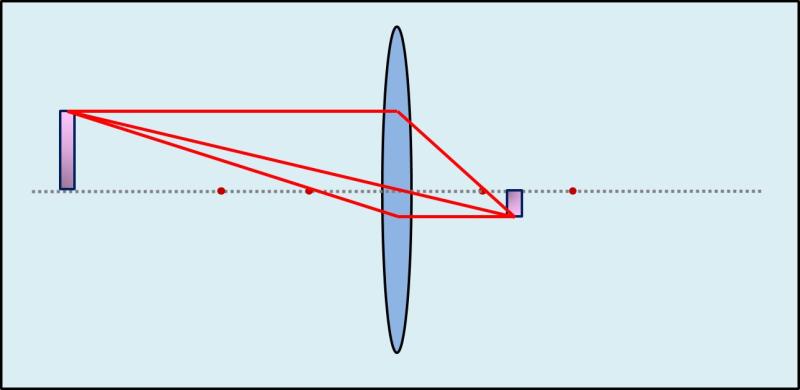
Man kann nicht in jedem Artikel von Null anfangen, daher setze ich jetzt einige grundlegende Kenntnisse zu konvexen Linsen voraus. Das Foto zeigt die Abbildung eines Objektes (links) durch eine konvexe Linse.

Da, wo sich der Parallelstrahl, der Mittelpunktstrahl und der Brennpunktstrahl auf der rechten Seite der Linse schneiden, dort entsteht eine umgekehrte Abbildung des Objektes. Es ist ein sogenanntes reelles Bild, welches sich auf einem Blatt Papier oder einer Leinwand usw. „einfangen“ lässt.
Betrachten wir jetzt einmal nur den Brennpunktstrahl, dann erschließt sich der Zusammenhang zwischen Brennweite und Vergrößerung sofort.
In der Grafik unten sieht man, dass der Brennpunktstrahl nach dem Austritt aus der Linse parallel zur optischen Achse verläuft und das in einem bestimmten Abstand. Dieser Abstand ist es, der über die Höhe des Abbildes bestimmt. Wo der Schnittpunkt mit den anderen Strahlen verläuft, das jetzt noch nicht so wichtig. Halten wir nur fest: die Höhe des Bildes ist sofort bekannt, sobald der Brennpunktstrahl zu sehen ist. Man beachte nun auf den folgenden Bildabschnitten was passiert, wenn der Brennpunkt sich von der Linse entfernt.
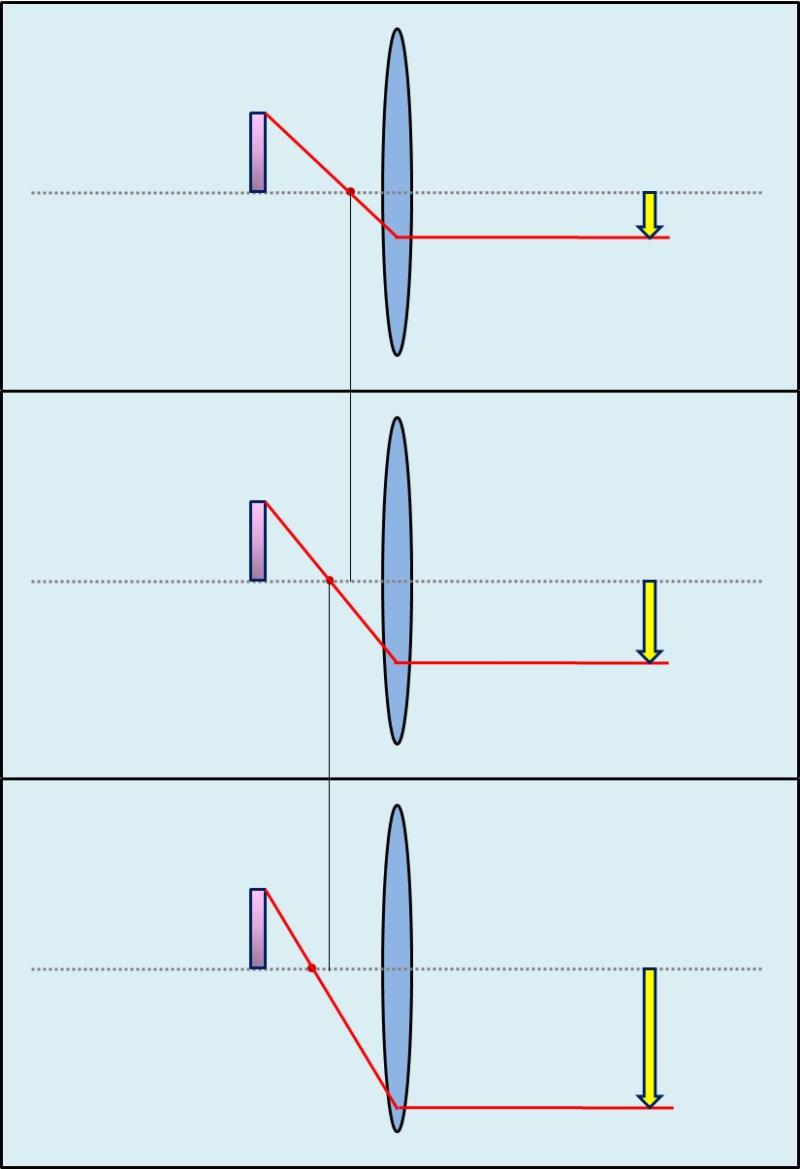
In den unteren zwei Bildern wird jeweils die Brennweite der Linse vergrößert. Das Objekt bleibt währenddessen immer an seiner festen Position. Mit jeder Verschiebung des Fokus weg von der Linse, ändert sich der Winkel, mit dem der Strahl auf die Linse trifft. Hierbei ist gut zu sehen: je weiter der Brennpunkt von der Linse entfernt ist, umso weiter der Abstand des Strahls von der optischen Achse nach dem Austritt. Demnach bewirkt eine Erweiterung Brennweite eine stärkere Vergrößerung.
Regel 2: Je größer die Brennweite, umso weiter entfernt sich das Bild von der Linse
Lässt man das Objekt an der gleichen Position und vergrößert die Brennweite der Linse, dann entfernt sich die Position der umgekehrten-reellen-Abbildung auf der anderen Seite der Linse:
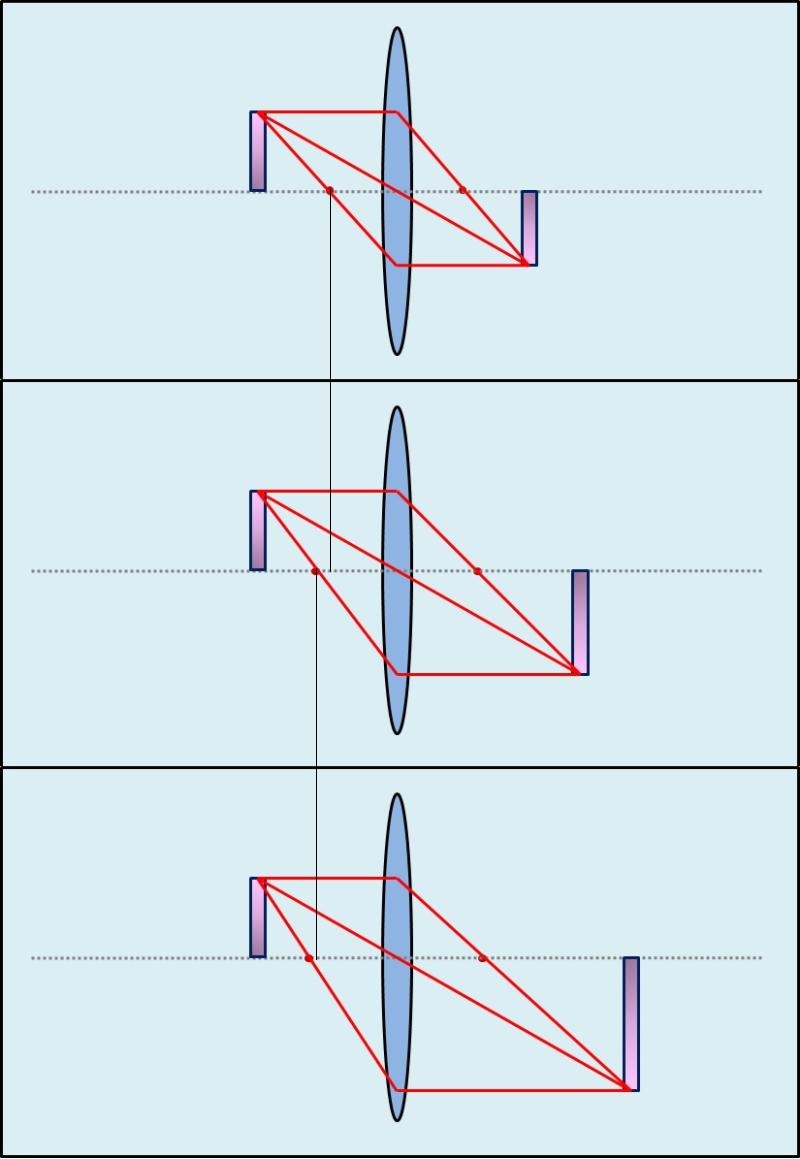
Beim Mikroskop ist die Situation genau anders herum. Dort ist durch den Tubus die Bildweite unveränderlich vorgegeben. Es muss daher die Entfernung des Objektes zum Objektiv verändert werden, damit ein scharfes Bild entsteht. Da das Objektiv ebenfalls befestigt ist, wird die Gegenstandsweite mit Heben oder Senken des Objekttischs verändert. Diesen kann man mit Hilfe des Grob- und Feintriebs in seiner Höhe verstellen.
Regel 3: Vergrößerung nur innerhalb der 2-fachen Brennweite
Verändert man den Abstand des Objektes zur Linse, dann ändert sich die Bildgröße und die Bildweite auf der anderen Seite. Hier lauten die wichtigsten Regeln:
Je näher das Objekt am Brennpunkt liegt, desto größer wird das Bild.
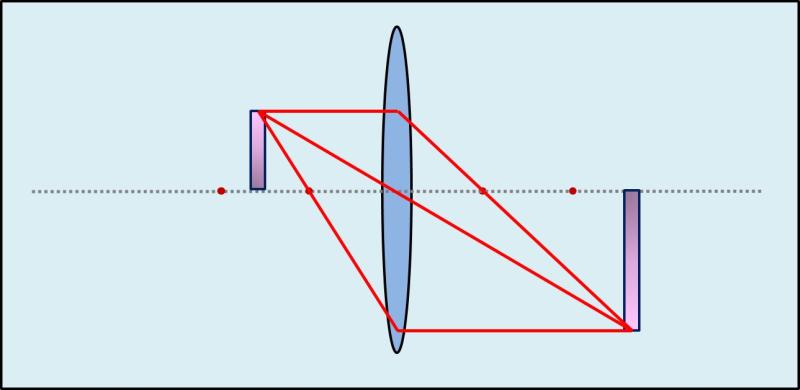
Liegt das Objekt um das Doppelte der Brennweite von der Linse entfernt, dann sind Objekt und Bild genau gleich groß.

Liegt das Objekt mehr als das Doppelte der Brennweite von der Linse entfernt, dann ist das Abbild eine Verkleinerung.
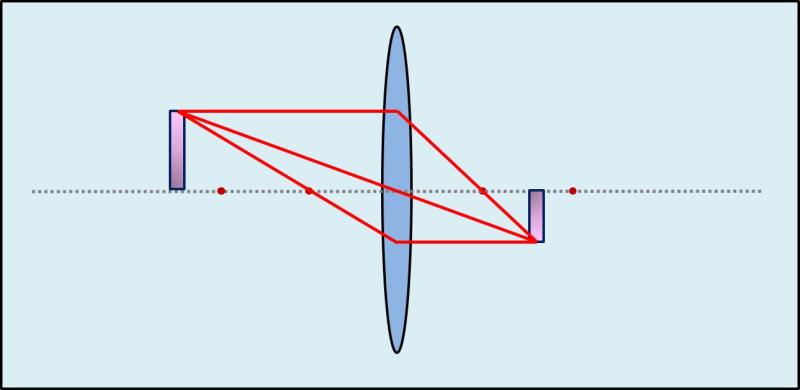
Je weiter das Objekt sich noch von der Linse entfernt, umso kleiner die Abbildung.
Rechnerische Betrachtung: Brennweite und Vergrößerung
Die grafischen Betrachtungen eignen sich besonders gut, um den Zusammenhang zwischen Brennweite und Vergößerung anschaulich darzustellen. Das ist gedächtnisgerecht und für das Verständnis einfacher zu zals abstrakte Formeln und Rechnungen. Dennoch erfordert das Leben meist auch mathematische Beweise, daher werde ich den Zusammenhang hier auch rechnerisch belegen.
Für die Erzeugung einer rellen Abbidung verwendet man die sogenannte Linsengleichung:

Die Formel der Linsengleichung lautet:
1/f = 1/b + 1/g
Definitionen:
g = Gegenstandsweite = wie weit entfernt steht das Objekt von der Linse
b = Bildweite = wie weit ist die reelle Abbildung von der Linse entfernt
f = Brennweite = Brennweite der Linse
Zur Vereinfachung erfolgt hier gleich eine Umstellung der Linsengleichung
g ist gesucht: g = (f*b) / (b-f)
b ist gesucht: b = (f*g) / (g-f)
f ist gesucht: f = (b*g) / (g+b)
Der Vergrößerungsfaktor errechnet sich:
b/g (Bildweite / Gegenstandsweite)
denn es gilt:
b/g = B/G (Bildgröße / Gegenstandsgröße)
Anwendungsbeispiel:
Nehmen wir an, wir platzieren ein Objekt 30 cm weit entfernt von einer konvexen Sammellinse. Wir wechslen immer nur die Linsen aus – bei verschiedenen Brennweiten. Wir schauen uns an, was mit der der Vergrößerung passiert. Die folgende Tabelle zeigt das Resultat:
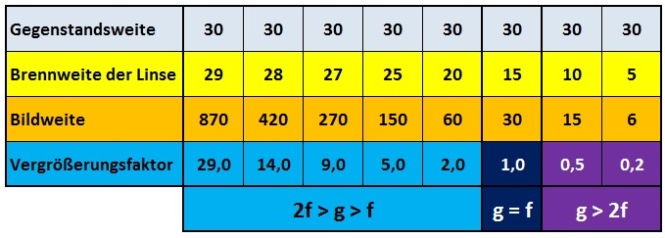
In der obigen Rechnung bleibt die Gegenstandsweite konstant bei 30 cm. Die erste Linse hat eine Brennweite von 29 cm. Damit steht das Objekt gerade so außerhalb des Fokus. Der Vergößerungsfaktor liegt hier bei 29X. Nun werden Linsen mit immer kürzerer Brennweite eingesetzt – was einer zunehmenden Entfernung von Brennweite und Objekt gleichkommt. Dabei sieht man, dass der Vergrößerungsfaktor immer kleiner wird, je größer die Distanz ist.
Wie in der grafischen Lösung bereits gezeigt, bestätigt sich auch rechnerisch, dass Bildgröße und Gegenstandsgröße genau dann gleich sind, wenn die Bildweite 2 mal so groß ist wie die Brennweite.
Man sieht ebenfalls, dass die Abbildung immer dann kleiner wird als das Objekt, wenn die Gegenstanstweite größer ist als das Doppelte der Brennweite.
Bei einem Mikroskop muss man natürlich umdenken. Dort wird die Bildweite immer durch die Länge des Tubus fix vorgegeben. Man kann sie auch nicht abändern, so dass sie als statischer Faktor fungiert. Daher müsste man die obigen Formeln anpassen, wenn man Berechnungen durchführen möchte. Die einzige Variable in dieser Anordnung ist beim Mikroskop die Bildweite. Das Objekt liegt auf einem Objekttisch und dessen Abstand zum Objektiv kann man mit Hilfe des Grob- und des Feintriebs verändern, um die richtigen Abstände für ein scharfes Bild herzustellen.
Erfinder / Entdecker der Linsengleichung
Als kleine historische Anmerkung… Ich habe versucht zu ermitteln, wer der Erfinder der Linsengleichung ist. Mich hat interessiert, wie lange sie schon bekannt war, bevor Enrst Abbe die Optik auf eine neue Ebene hob. Laut dieser Seite hat der englische Physiker und Astronom Edmond Halley die im Jahr 1690 die Abbildungsgleichung für optische Linsen abgeleitet. Das passiert wirklich selten, das gesamte Internet konnte mir keine sichere Antwort liefern. Vielleicht findet ihr es ja heraus 😉
Objekt innerhalb der Brennweite – virtuelles Bild
Bei der Vergrößerung als virtuelles Bild fungiert die Linse als Lupe. Die Berechnung der Vergrößerung einer Lupe ist deutlich einfacher als bei der optischen Abbildung. Die Formel lautet:
Vergrößerung = 25 cm / Brennweite in cm
Die 25 cm ist die deutliche Sehweite des menschlichen Auges. Sie ist in dieser Formel eine Konstante. Die Brennweite dagegen ist der Nenner. Man muss kein Mathematiker sein, um erkennen, dass die Vergrößerung umso größer ist, je kleiner die Brennweite.
Im Mikroskop fungiert das Okular wie eine Lupe. Sie vergrößert die reelle Abbildung aus dem Objektiv zu einem virtuellen Bild.
Auch dieses Szenario möchte ich mit einigen Grafiken verdeutlichen:
Regel: je kürzer die Brennweite, desto höher die Vergrößerung.
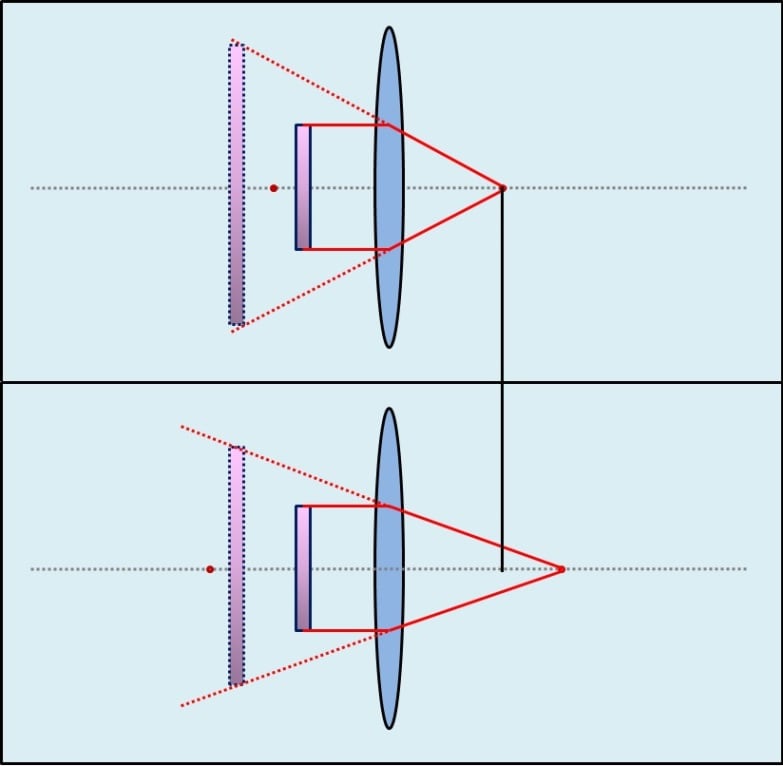
Die Grafik oben zeigt die gleiche Linse. Im unteren Teil wurde die Brennweite verlängert. Dies hat zur Folge, dass sich die Strahlen nach Austritt in einem flacheren Winkel im Brennpunkt schneiden. Dadurch erscheint das virtuelle Bild kleiner.
Hier eine weitere Grafik, wo man beide Brennpunkte in einem Bild sehen kann:

Die blauen Linien entstehen bei einer kürzeren Brennweite. Das virtuelle Bild erscheint dem Betrachter dadurch größer.
Im Aufbau des Lichtmikroskop finden sich übrigens alle beiden Arten von Vergrößerungsmethoden. Das Objektiv erzeugt das reelle-umgekehrte Bild, das Okular vergrößert dieses zu einem virtuellen Bild.