Összefüggés a fókusztávolság és nagyítás között elmagyarázva
Milyen befolyása van a fókusztávolságnak egy konvex domború lencse nagyítására? Erre a kérdésre két válasz van, mert a mikorszkópban két fajta módon lehet nagyítani.
Mielött kezdjük: fókusztávoolság = gyújtótávolság
Amikor a tárgy a lencse fókusztávolságán kívül fekszik akkor egy valódi kép / leképzés készül. Ilyenkor egy nagyobb fókusztávolság magasabb nagyitási fokot okoz.
Amikor a tágy a lencse fókusztávolságán belül fekszik, akkor egy virtuális kép készül. Ilyenkor egy rövid fókusztávolság termel nagyobb képet.
Tartalom:
1. Tárgy a fókusztávolságon kívül – valódi kép
Az összefügést a fókusztávolság és a nagyítás között a „távolságtörvényben“ vagy a „lencsetörvényben“ van mefogalmazva. De az egy számolás, amit fejben nem lehet könnyen követni. Ezért én grafikus módon akarom bemutatni az össezfüggéseket. Ezen az úton könnyebben érthetö és nem kell mindig újbol számolgatni, ha cserélödik egy változó.
Szabály: Mennél nagyobb a fókusztávolság, annál magasabb a nagyítási fok
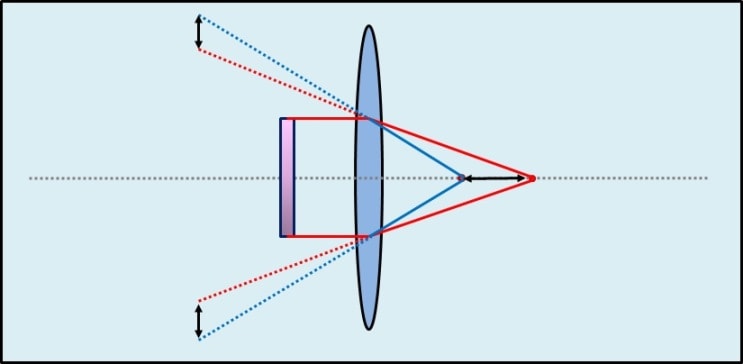
A fotó egy tárgynak a leképzését mutatja egy konvex domború lencsével. Ott ahol a sugrak összetalálkoznák a lencse jobb oldalán, ott készül egy éles, fejen álló kép. Ezt nevezik valódi képnek, mert papírra vagy egy vászonra lehet vetíteni.
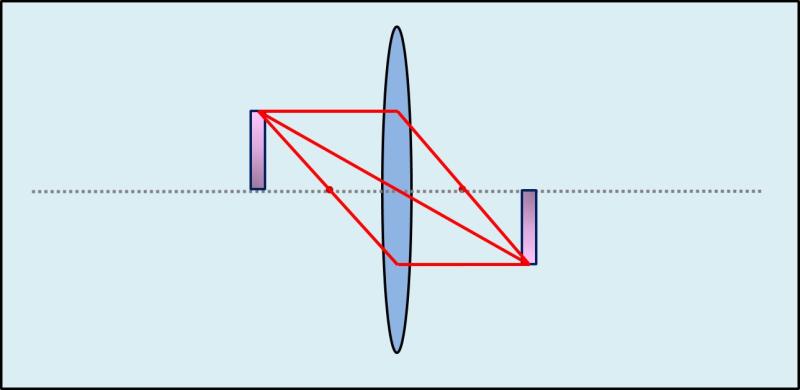
Most nézzük csak azt a sugarat, ami a képoldalon párhuzamosan megy az optikai tengelyhez. Ez mutatja a leggyorsabban az összefüggést. A lenti rajz felsö részében látható, hogy a fókuszpont-sugár úgy lép ki, hogy egy bizonyos távolságban párhuzamosan megy az optikai tengely mellett. Ez a távolság határozza meg a leképzésnek a magasságát. Ez a tudás egyenlöre elég. Hogy hol vágja a többi sugarat, az most nem lényeges.
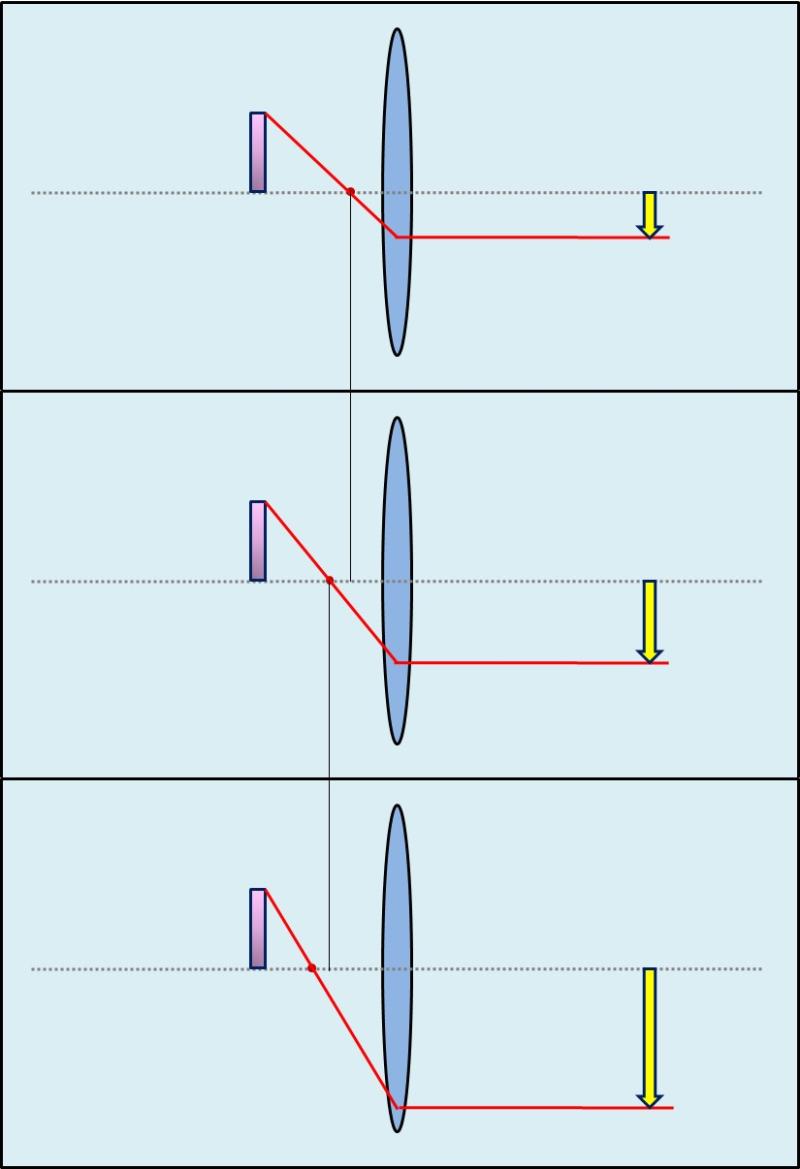
A kép also két harmadában a fókuszpont mindig egy kicsit eltávolódik a lencsétöl. A tárgy megtartja a helyét. Mindig, amikor a fókuszpont eltolódik, akkor más szögben esik be a lencsébe a sugár. Ezzel a kilépésnél eltávolódik az optiakai tengelytöl. Ez bizonyítja azt, hogy egy nagyobb fókusztávolság nagyobb nagyítást okoz.
Szabály: Mennély nagyobb a fókusztávolság, annál messzebb a képtávolság a lencsétöl és annál nagyobb a kép
Ha a tárgy tartja a helyét és a fókusztávolság növekszik, akkor a kép a lencsétöl egyre messzebre jön létre.
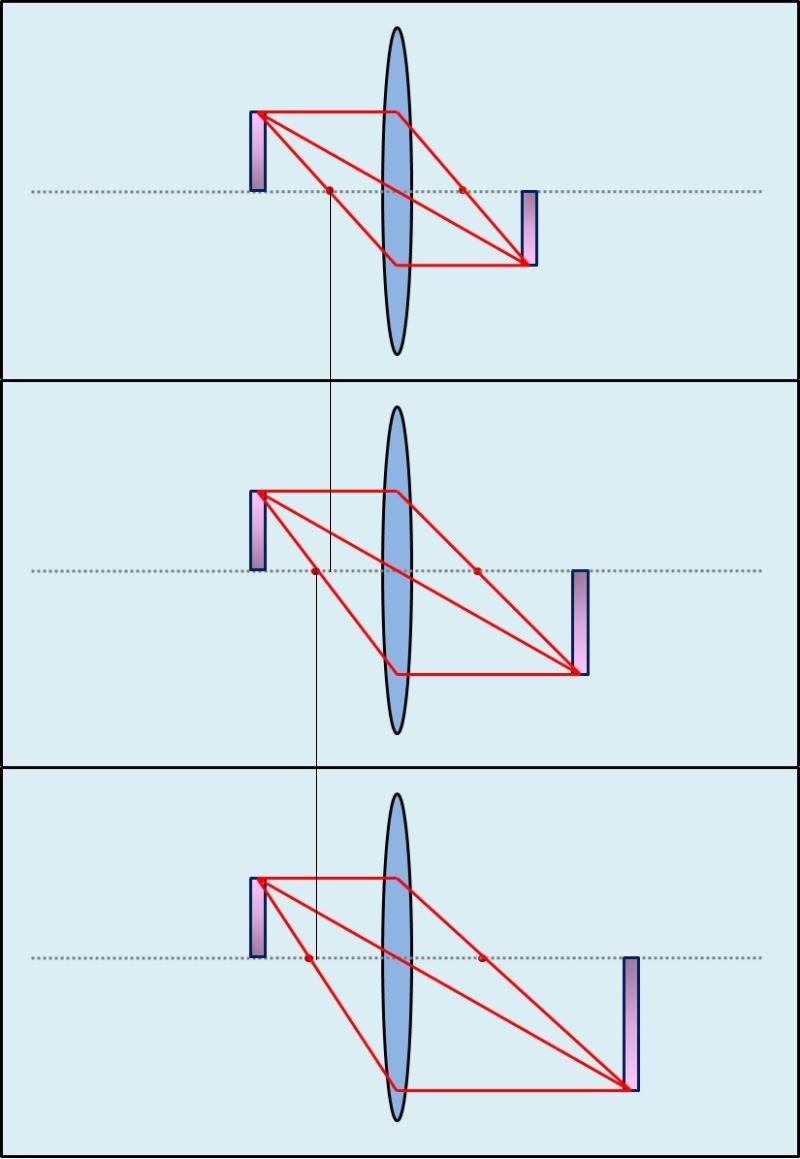
Ez a mikroszkóban viszont fordítava van. Ott a képtávolság a tubusnak a hosszához van kötve. Ugyanúgy az objektiv is rögzítve szokott lenni. Ezért mindig a tárgyat kell mozgatni a tárgyaszallal.
Szabály: Nagyítás csak a kétszeres fókusztávolságon belül
Amikor a tárgynak a helyét változtatják, akkor a képtávolság és a kép nagysága változik. Erre a helyzetre is van egy néhány fontos szabály:
Mennél közelebb a tárgy a fókuszhoz, annál nagyobb a kép.
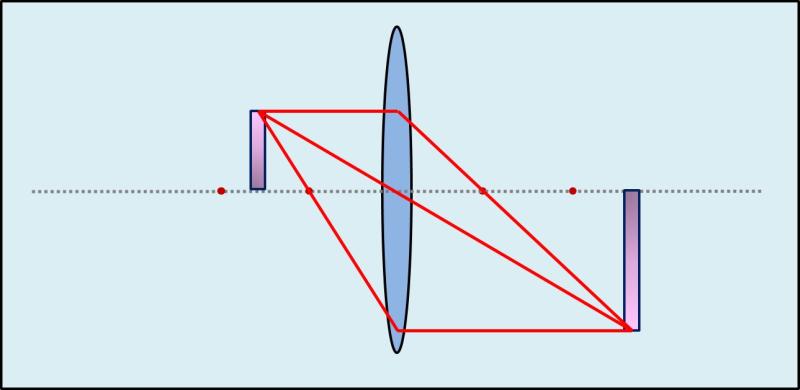
Viszont! – Ha a tárgy a fókuszban áll, akkor nem jön létre kép!
Ha a tárgy pontosan a kétszeres fókusztávolságban fekszik, akkor a kép egyforma nagy.
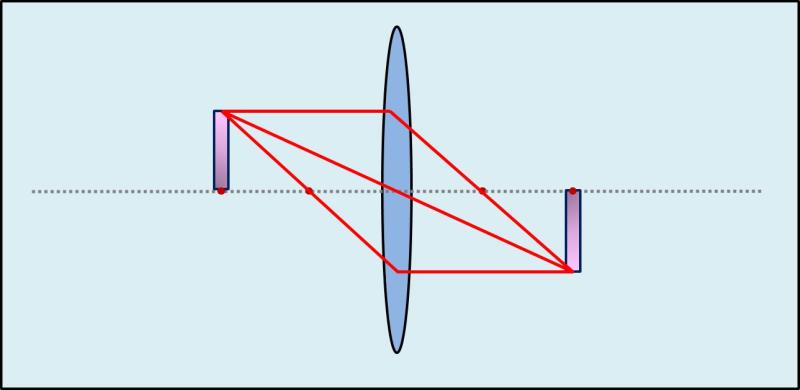
Ha a tárgy a kétszeres fókusztávolságnál messzebre van, akkor a kép kissebb lessz mint a tárgy.
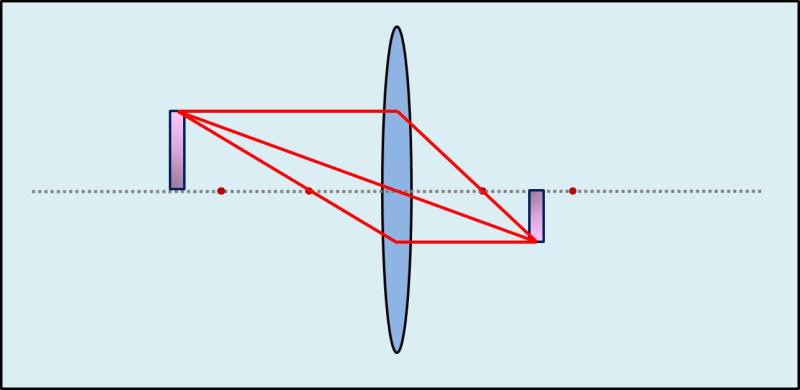
Mennél messzebra van a tárgy, annál kissebb lessz a kép
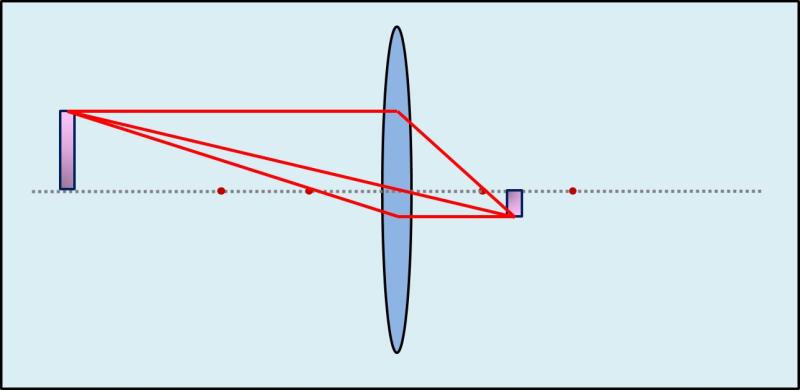
2. Tárgy a fókusztávolságon belül – virtuális kép
Amikor a tárgy a fókusztávolságon belül fekszik, akkor a lencse úgy hat mint egy szokásos nagyító és egy virtuális képet készit. Egy nagyítónak a hatását kiszámolni aránylag egyszerü:
Nagyítas = 25 cm / fókusztávolság (cm)
A 25 cm az emberi szemnek a éles látásitávolsága. Ebben a számításban a 25 cm egy állandó. A fókusztávolság az osztó, ezért nem kell lenni matematikusnak, hogy rögtön lássuk:
Mennél kissebb a fókusztávolság, annál magasabb a nagyítás
A mikroszkópra vonatkozva: az okulár müködik úgy mint a nagyító. Az készíti a virtuális képet.
Ezt a tényt is be lehet bizonyítani képekkel:
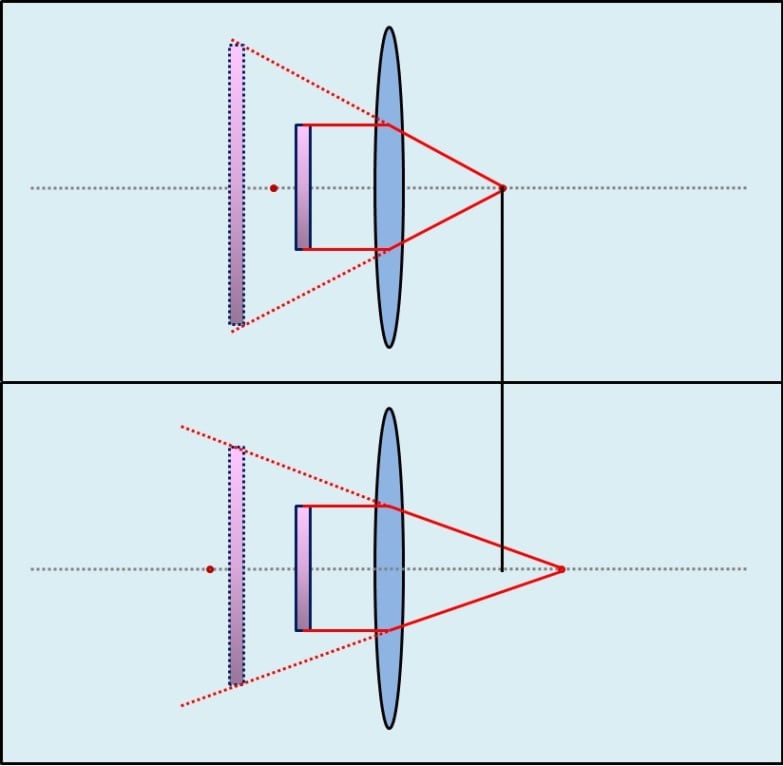
A fönti kép ugyanzt a lencsét mutatja. A lenti részben a fókusztávolság nagyobb lessz. Ez megváltoztatja a szöget, amiben a fénysugarak a fókuszba beesnek. Ettöl a virtuális kép kissebb lessz.
Itt még egy másik kép, ahol egyben lehet látni a fókusz eltolásának a hatását.