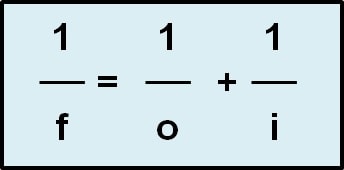In this article, I explain the correlation between the magnification factor and the focal lenght / focal distance of a convex collecting lens.
You will see both mathematical explainations and graphical demonstrations.
**********
Summary:
- For the optical illustration of an object (=real image) – a higher focal length means a higher magnification factor.
- For the optical enlargement of an object (=virtual image) – a brief focal length means a higher magnification.
This difference depends on the placement of the object – within or outside of the focal length / focal distance of the convex collecting lens.
Object outside of the focal distance – real image
The corellation between magnification an focal lenght is described in the lens equation formula. But this calculation is too abstract to illustrate the topic. It is the easier way to exemplify it graphically and then to “brood” over the formula and always to calculate from new, when a variable has changed.
For the optical illustration of an object, these rules apply:
Ruke 1: The higher the focal lenght, the higher the magnification
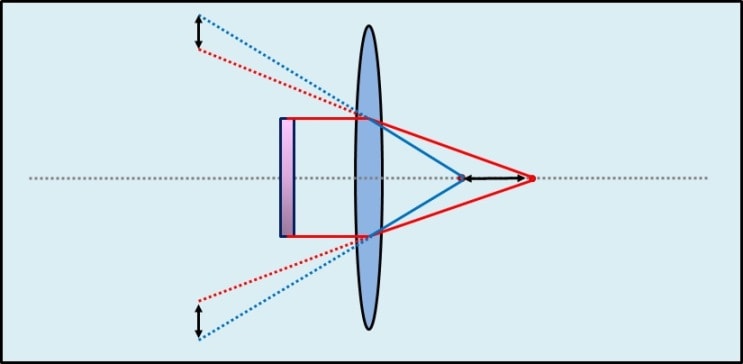
The pictures shows the optical illustration of an object with a convex collecting lens.
On the left side is the object. On the other side of the lens, there is a point, where the parallel beam, the focal ray and the center ray meet. This is where the illustration of the object is projected on an surface, like the cinema screen, ot a sheet of paper. See the example:

Betrachten wir jetzt einmal nur den Brennpunktstrahl, dann erschließt sich der Zusammenhang zwischen Brennweite und Vergrößerung sofort.
Now, let´s just analize the focal ray, so you can see easily, the correlation between the focal distance and the magnification factor.
The follwing graphic shows, the the focal ray becomes a parallel beam, after its exit from the lens. It is parallel to the optical axis and it runs in a certain distance to it. This distance is equal to the prospective height of the optical illustration / real image.
Let´s see, what happens if the distance of the objetc to the lens stays the same and only the focal distance is changing:
We see, that the longer the the focal length is, the bigger will be the height of the real image. This proves, already, what I said at the beginning: a larger focal distance, increases the magnification factor.
Rule 2: The larger the focal distance, the larger the distance of the real image form the lens
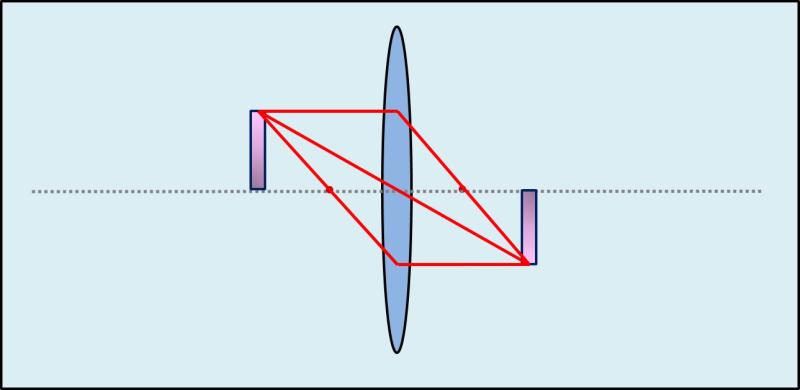
Now we take a look an what happens with the real image, when the distance between object and lens stays the same and we change the focal length.
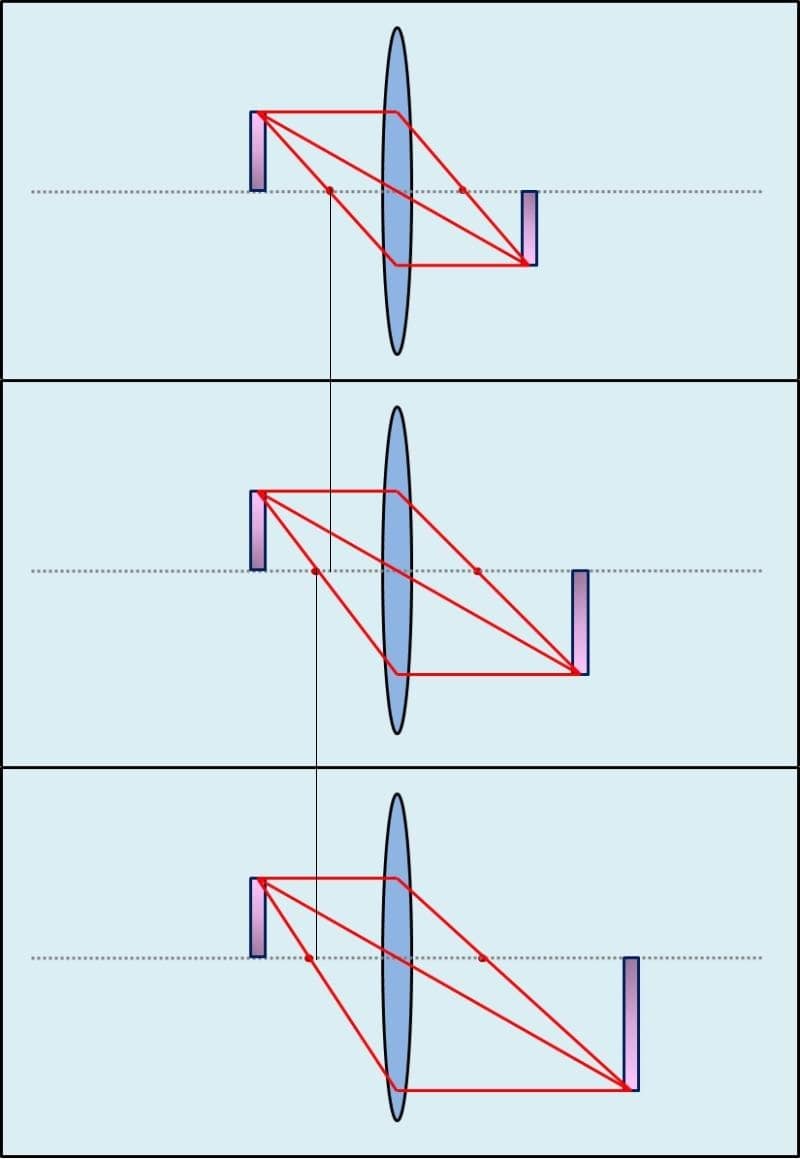
The result is, that the position of the real image is farther, the higher the magnification is.
In a microscope, we find the other situation. The distance of lens & image has to be the same, as one can´t change the length of the lens tube. Thus, we have to change the distance between the the object and the objective lens, by moving the stage / cross table to get a clear image.
Rule 3: Enlargement only within 2X of the focal distance
Now we begin to change the distance between the object and the lens. This also influences the magnification and we see, that some different rules apply:
The closer the object to the focal pointis, the higher is the magnification rate.
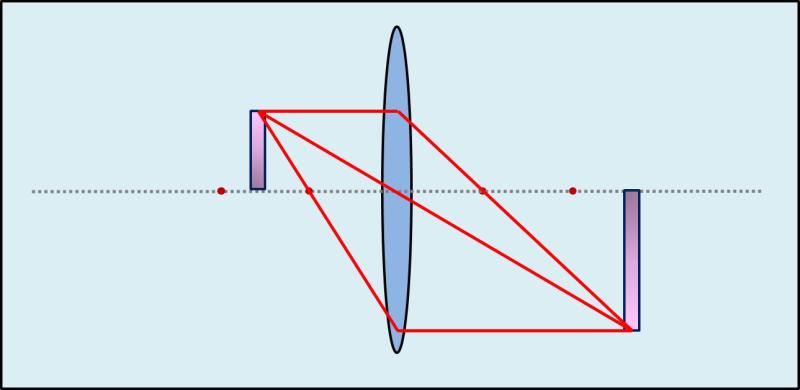
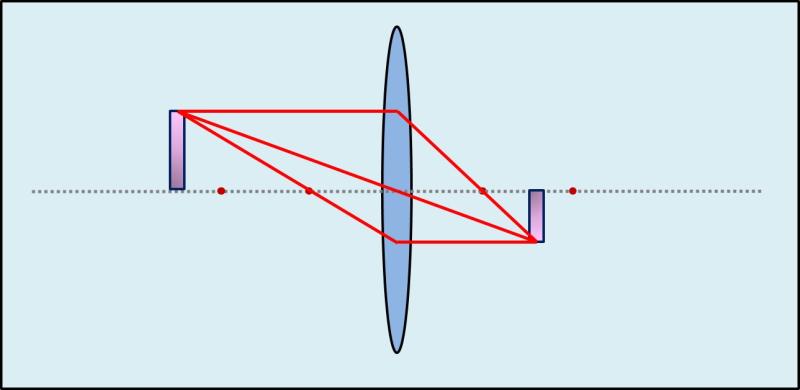
If the object is placed 2X of the focal length, then the object and the real image will have the same size.
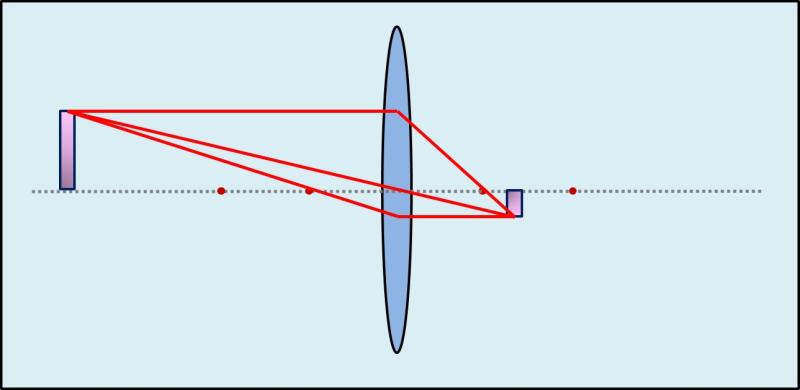
If the objet´s distance is farther than 2X-focal lenth, then the real image becomes demagnified – is smaller than the object.
The farther the object from the lens, the smaller is the real image
Calcualtiv analysis – the “thin lens equations” formula
The grafical demonstration is much easier to use and to memorize the the optical illustration rules. But now, I would also like to explain the lens equation formula and prove the rules by it.
thin lens equations formula
Thins lens equation formula:
1/f = 1/o + 1/i
Definitions
o = object distance = how far is the object from the lens
b = image distance = how far is the image from the lens
f = focal length = focal length of the lens
To make it simpler – some variotions of the formula:
o is searched: o = (f*i) / (i-f)
i is searched: i = (f*o) / (o-f)
f is searched: f = (i*o) / (o+i)
The magnifiaction factor can be calculated with this formula:
i/o (image distance / object distance)
as….
i/o =I/O (I = image size / O = object size)
Calculation example:
Let´s say, we place an object in a distance of 30 cm from a convex lens. We only change the lenses, which have different focal lengths. Here the results:
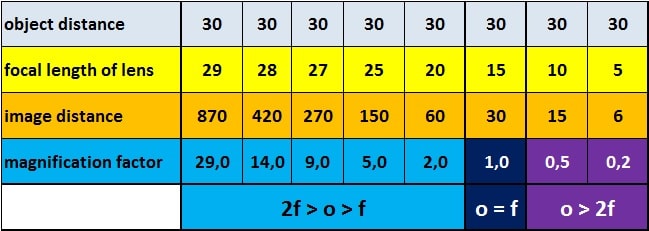
Like already shown in the graphical illustration, the calculation proves, that object size and image size are identical, when the object distance is 2X-focal length.
It also confirms, that if the object distance is larger than 2X focal length, the image becomes a demagnification.
Object within the focal distance – virtual image
When the object is placed within the focal distance, the lens works lika a magnifying glass.
The calculation for a magnifier is much easyer than for optical illustration. The formula is:
magnification = 25 cm / focal length of the lens (in cm)
The 25 cm is the conventional closest distance of distinct vision for the human eye. This distance is a constant in the calculatio and never changing. Therefore, one doesn´t have to be a mathematical genius to see, that the smaller the focal length is, the higher will be the magnification.
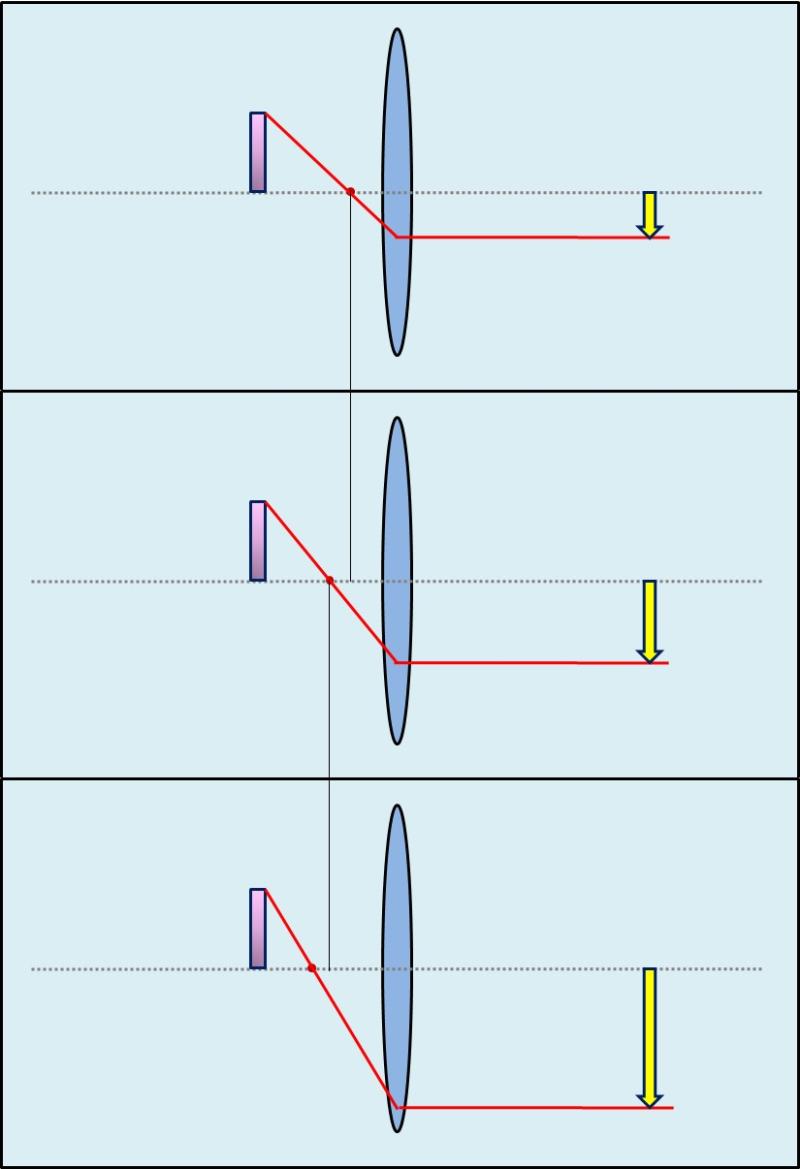
Please see the graphical illustration:
Rule: the shorter the focal length, the higher the magnification factor
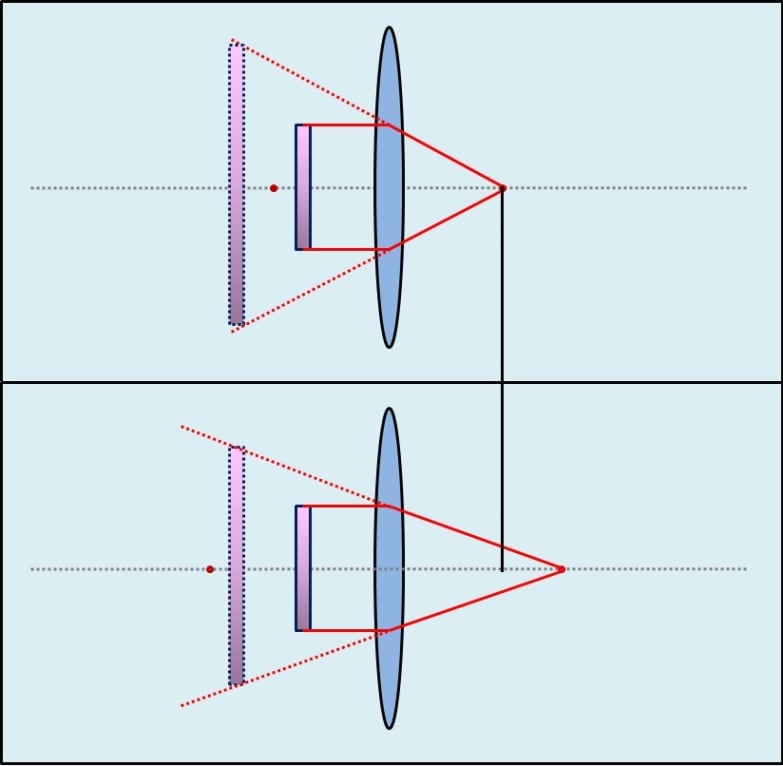
The graphic shows, that the length of the focal distance changes the angle, in which the light is refracted.
The shorter the focal lenght, the steeper the angle of the refraction: